איך מחשבים שטח דלתון?
מבט מהיר על איך מחשבים שטח דלתון?
מהו הדלתון?
הדלתון ביחד עם המקבילית, הריבוע, המלבן והמעויין לוקח חלק במשפחת המרובעים – המצולעים בני ארבעת הצלעות.
הדלתון מוגדר כמרובע בעל שני זוגות של צלעות סמוכות השוות זו לזו.
תכונה זו מייחדת את הדלתון ומביאה לידי ביטוי תכונות נוספות.
ישנם שני סוגים של דלתון – דלתון קמור ודלתון קעור.
הדלתון הקמור:
הדלתון הקמור הוא הדלתון שכולנו מכירים – ארבעת צלעותיו פונות כלפי חוץ.
כתוצאה מתכונות הדלתון הייחודיות, ניתן לומר כי הדלתון מורכב למעשה משני משולשים שווי שוקיים ולכן, האלכסונים בהתאם כבסיס המשולש וכגובה, חוצה הזווית והתיכון היורד אליו.
את הדבר ניתן לראות בקלות בשרטוט:
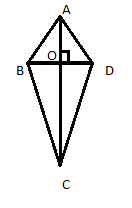
בדלתון ABCD נוכל לראות:
AB = AD
BC = CD
BO = DO
זווית AOB = 90
זווית BAO = זווית DAO
הדלתון הקעור:
הדלתון הקעור הוא הגרסה הפחות מוכרת והטיפוסית של הדלתון.
בדלתון הקעור אחד מזוגות צלעות הדלתון השוות פונות לפנים המרובע ויוצרות מעין צורה של לב.
באופן כזה, באמצעות ציור האלכסון החיצוני נקבל למעשה שני משולשים שווי שוקיים, שנמצאים אחד בתוך השני.
הדבר נראה באופן:
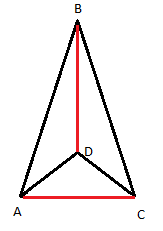
בדלתון ABCD נוכל לזהות בקלות:
AD = DC
AB = BC
אלכסוני הדלתון הם AC ו-BD
הזווית ABD = הזווית CBD
אם נמשיך את האלכסון BD, נקבל גובה לצלע AC.
איך מחשבים שטח דלתון?
עכשיו כשאנחנו קצת יותר מכירים את הדלתון, נוכל לגשת לחישוב השטח שלו.
חישוב שטח דלתון הוא פעולה לא יותר מידי מסובכת – מדובר פשוט בנוסחה.
על מנת לחשב את שטח הדלתון, נכפיל את אלכסוני הדלתון ואת המכפלה נחלק בשתיים.

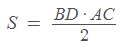
גם כאשר מדובר בדלתון קעור, נבצע את הפעולה הזהה באותו האופן בדיוק.
שאלות לדוגמא:
על מנת לוודא שהבנתם את הנוסחה כראוי, ריכזנו עבורכם שני תרגילים כך שתוכלו לתרגל את החומר כראוי.
בהצלחה!
תרגיל 1-
נתון –
AD = DC
AB = BC
BD = 8
AC = 6

חשבו את שטחו של המרובע.
פתרון –
אמנם לא נאמר לנו מפורשות מהי הגדרת הצורה, אך כיוון שנתון לנו מרובע בעל שני זוגות צלעות שווים, ניתן להסיק כי מדובר בדלתון.
כעת, נוכל להציב בנוסחה ולקבל את התשובה.
![]()
וסיימנו!
תרגיל 2-
נתון –
דלתון ABCD
AB = DB = 6
BC = DC = 9
BD = 10
- מצאו את אורך האלכסון AC
- מצאו את שטחו של הדלתון
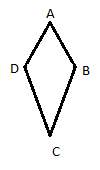
פתרון –
סעיף א' – ראשית נתחיל בציור בניית עזר ונגדיר את נקודה O.

כעת, נוכל להתחיל לחשוב על הנתונים.
בהתאם להגדרת הדלתון, האלכסון AC משמש כגובה במשולש ADB ולכן ניתן להסיק כי BO = DO.
כלומר, שני חצי האלכסון BD שווים ל-5.
את מציאת אורכו של האלכסון AC נחלק לשני שלבים – מציאת אורכו של OA ומציאת אורכו של OC ולבסוף, חיבורם.
את חישוב האורכים נבצע כמובן באמצעות משפט פיתגורס.
חישוב אורך המקטע OA –
![]()
![]()
![]()
חישוב אורך המקטע OC –
![]()
![]()
![]()
וכעת לתשובה הסופית – אלכסון AC שווה לסכומם של המקטעים OC ו-OA. OC = 10.3.
סיימנו!
סעיף ב' – כעת, יש לנו את שני אורכי האלכסונים וכל מה שנותר זה רק להציב אותם בנוסחה שלנו בשביל להגיע לשטח הדלתון – ![]()
סיימנו!
טיפים ללמידה נכונה:
עולמות הגיאומטריה לוקחים חלק משמעותי במיוחד בתוכנית הלימודים התיכונית לקראת הבגרות במתמטיקה.
ולכן, חשוב להעמיק בחומר, לוודא הבנה ולדאוג להשקיע במקצוע במהלך כל שנת הלימודים – לא מומלץ לחכות לשבוע שלפני הבחינה.
תעברו על התרגילים בכיתה ושיעורי הבית, תשבו עם חברים ותשמעו על הדרך שבה הם מבינים את החומר ותמצאו גם את הדרך האישית שלכם.
לחלק מאיתנו עוזר לפתור הרבה תרגילים, לאחרים נוח להסביר את החומר התיאורטי בעל פה ולחלק אפילו להמציא עליו שיר או סיפור.
אם אתם מסתבכים בלימודים ומעוניינים בסיוע – יכול להיות שכדאי לכם לפנות למורה פרטי.
באתר שלנו תוכלו להנות ממבחר אדיר של מורים למתמטיקה ומקצועות רבים נוספים שיותר מישמחו לעזור לכם, ללמד וכמובן – להפוך את הלימודים למעט יותר מאתגרים ואפילו למהנים.
בהצלחה!


