איך מחשבים שטח של טרפז?
מבט מהיר על איך מחשבים שטח של טרפז?

אז מה זה בכלל שטח טרפז?
טרפז הוא מרובע בעל זוג צלעות מקבילות וזוג צלעות לא מקבילות, כאשר אלה יכולות להיות שוות או לא שוות כאחד.
כחלק מתוכנית לימודי הגיאומטריה בבתי הספר היסודיים והתיכוניים, נדרש מהתלמידים ברחבי הארץ להכיר את תכונות הטרפז, סוגי הטרפזים השונים וכמובן – את הנוסחה לחישוב שטח הטרפז.
הנושא יכול להיראות עבור רבים ללא ההכנה המוקדמת כמלחיץ ומרתיע, אבל בסופו של דבר – עם קצת תרגול וההסבר המדויק והנכון, כל אחד יכול להפציץ במבחן.
אנחנו כאן בשביל לעזור ולחלוק איתכם את כל הסודות ובתכלס, כל מה שאתם צריכים לדעת על המרובע המיוחד הזה.
הטרפז כאמור מורכב משתי צלעות מקבילות הנקראות בסיסים ושתי צלעות לא מקבילות שנקראות שוקיים.
על מנת להוכיח שהמרובע שעומד לפניכם הוא טרפז, כל מה שעליכם לעשות למעשה, זה להוכיח שהמרובע הזה בעל זוג צלעות מקבילות וזוג צלעות נוסף שאינן מקבילות.
תכונות הטרפז
לטרפז ישנן כמה תכונות, שיכולות לעזור לכם בפתירת תרגילים כאלה:
- זוויות חד צדדיות – סכום זוויות חד צדדיות בטרפז שווה ל-180 מעלות.
- גבהים – במידה ואתם מעוניינים לחשב את מקטע הבסיס הקצר, תוכלו להיעזר בחישובים בהורדת גבהים מקודקודי הבסיס הקצר לעבר הבסיס הארוך.
כך תתחמו למעשה מלבן, שיכול לעיתים להיות שימושי בחישובים.
משפט פיתגורס אגב, יכול תמיד להועיל.
אז איזה סוגי טרפזים בכלל יש?
ישנם כמה סוגים של טרפזים שכנראה יצא לכם להיתקל איתם. היכרות ראשונית של סוגי הטרפזים השונים יכולה לעזור לכם לגשת לשאלות עם ידע מקדים נוח ושימושי שייקל עליכם בעת המענה. אז איזה סוגי טרפזים חשוב להכיר?
טרפז ישר זווית – טרפז ישר זווית מאופיין בכך שאחת הצלעות שלו אנכית לבסיסים. כך, הוא יוצר עם אלה זווית של 90 מעלות. בנוסף, אם תורידו אנך מקודקוד המקשר את הצלע השנייה עם אחד הבסיסים לבסיס השני, הצורה שתקבלו תהיה מלבן.
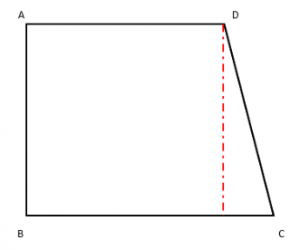
טרפז שווה שוקיים – בטרפז שווה שוקיים, כפי שמשתמע משמו הוא זוג השוקיים ששוות זו לזו. כיוצא בזאת, גם הזוויות הסמוכות בבסיסים שוות זו לזו.
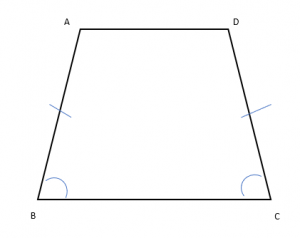
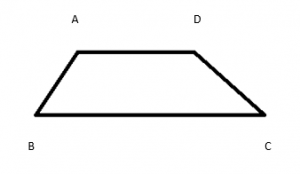
מקבילית – טרפז בו השוקיים מקבילות זו לזו, נוסף על זוג הבסיסים הוא למעשה המקבילית עליהן כבר יצא לכם ללמוד. מדובר בטריק הוכחה שימושי!

אז איך נחשב שטח טרפז?
אחרי שאתם מכירים קצת את תכונות הטרפז, כל מה שנשאר לכם להכיר זה רק את המשוואה הפשוטה לחישוב שטח טרפז.
המשוואה אולי לא תהיה אינטואטיבית בהתחלה, אבל עם קצת תרגול, אתם תשימו לב שהיא באה לכם באופן טבעי בפתירת התרגילים השונים בספרי הלימוד.
אז מהי המשוואה?
![]()
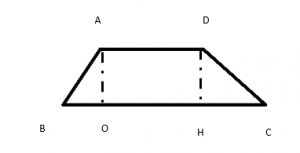
נגדיר טרפז ABCD.
AD || CB
AB || DC
DH מאונך לבסיס BC
משוואת שטח הטרפז שלנו תהיה:
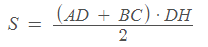
או במילים מעט פשוטות יותר – שטח טרפז שווה לסכום הבסיסים כפול הגובה לאחד הבסיסים חלקי שתיים.
עכשיו כשאתם מכירים את הנוסחה מקרוב, הגיע הזמן לקצת דוגמאות!
תרגיל לדוגמא 1
נתון טרפז ABCD:
AD || BC
DC = 5 ס"מ
AD = 4 ס"מ
BA = 6 ס"מ
ישר DH מאונך ל-BC ושווה ל-3 ס"מ
מצא את שטח טרפז ABCD.
פיתרון:
בואו נתחיל מלהתבונן בתרשים.
אנחנו יכולים לזהות כי בסיסי הטרפז הם AD ו-BC, כיוון שנתון לנו שהם מקבילים.
בנוסף, יש לנו נתונים על אורכי השוקיים, אחד הבסיסים וגובה לאחד הבסיסיים.
במילים אחרות, הדבר היחיד שחסר לנו בשביל למצוא את שטח הטרפז הוא כמובן הבסיס BC.
אז מה נעשה?
את הפתרון נחלק לשלושה שלבים, כאשר כל אחד מהם נועד לסייע לנו למצוא מקטע אחר מהבסיס BC שניתן לנו.
נתחיל בשרטוט בניית עזר של גובה DH וגובה נוסף (שלא ניתן לנו), AO.
אמנם לא נתונים לנו פרטים עליו, אבל כיוון שמדובר בשני קטעים מקבילים שעוברים בין שני קטעים מקבילים, ניתן להסיק כי ADHO הוא מלבן וכיוצא בזאת – DH = AO.
כעת, נוכל להתחיל בחישובים.
ראשית, נחשב את HC באמצעות משפט פיתגורס.
נתון לנו כי DC = 5 ס"מ וכי DH = 3 ס"מ. כעת, נוכל להציב במשפט פיתגורס.
![]()
נעביר אגפים ונציב:
![]()
מכאן נוכל לחשב ולהבין ש-CH = 4 ס"מ.
- שנית, נעבור לחשב את OH. כיוון שהבנו קודם ש-OADH הוא למעשה מלבן, ניתן להסיק -OH שווה בגודלו ל-AD. כיוון שנתון לנו ש-AD = 4 ס"מ, כעת אנחנו יודעים ש-OH = 4 ס"מ.
- לבסוף, נרצה לחשב את מקטע BO בדומה לאופן שבו חישבנו את HC – פיתגורס. אנחנו יודעים את AO, BA נתון לנו וכל מה שנשאר לנו כעת זה רק להציב במשפט פיתגורס ולמצוא את BO.
![]()
כעת נבודד את BO ונציב:
![]()
ומכאן – BO = 5 ס"מ.
כעת, על מנת למצוא את הבסיס BC שחסר לנו, כל מה שנותר לעשות זה רק לחבר את הקטעים:
![]()
וכעת, כשמצאנו את הבסיס, נוכל להציב את הנתונים ולמצוא את שטח הטרפז שלנו.
![]()
![]()
מכאן, שטח הטרפז ABCD שווה ל-25.5 סמ"ר.
סיימנו!
אז מה עוד כדאי לדעת?
בתכלס, אם אתם שואלים אותנו, לקרוא את החומר זה חשוב ומשמעותי.
אבל, בשביל להכיר אותו כמו שצריך, לדעת אותו לדקויות ובסוף לקבל ציון גבוה במבחן צריך לא רק לשנן אלא גם ליישם.
אנחנו ממליצים לכם לתרגל את כל השאלות שיש לכם בנושא הטרפזים ולמעשה, בכל נושא שיעלה לכם במתמטיקה כמה שיותר, עד לנקודה שבה תרגישו בנוח עם החומר.
תשאלו שאלות, תגדילו ראש ותתעכבו על נקודות שאתם לא מבינים – רק ככה תוכלו להשתפר.
ומה אם אני לא מסתדר בכוחות עצמי?
בתכלס, מתמטיקה זה לא מקצוע קל.
כיום, יותר ויותר תלמידים נעזרים במורה פרטי למתמטיקה והאמת היא, שזה ממש הגיוני.
המעטפת שבתי הספר נותנים כיום במתמטיקה לתלמידים השונים היא חלשה ועבור רבים מהתלמידים, היא פשוט לא מספיקה.
אם אתם מחפשים את המעבר, שואפים לציונים הכי טובים ולא מפחדים מעבודה קשה – המורים שלנו יותר מישמחו לעזור.
למורים שלנו במתמטיקה יש ידע נרחב במתמטיקה, אבל יותר מכך – הם בעלי ניסיון עשיר שנים בלימוד.
אז למה אתם מחכים? תמצאו את המורה שלהם עוד היום!


