חוקי לוגריתמים
מבט מהיר על חוקי לוגריתמים

חוקי לוגריתמים
חוקי לוגריתמים יכול להיות ללא ספק נושא מפחיד במיוחד כשאתה רק מתחיל ללמוד אותו – הסימונים חדשים, החישובים עוד לא אינטואטיבים והחוקים נראים קצת מוזרים.
אבל האמת היא, שאם אתם שואלים אותנו, לא מדובר בעניין יותר מידי מסובך.
לוגריתמים אמנם לא ישמשו אתכם ביומיום, אבל במידה ותעסקו בכימיה, מתמטיקה ביולוגיה, סטטיסטיקה ואפילו פסיכולוגיה מחקרית – כנראה שיהיה מדובר עבורכם במיומנות שימושית.
וחוץ מזה – זאת מיומנות שתפתח לכם גם קצת את המחשבה.
בשביל לסיים את תוכנית הלימודים התיכוניים בהצלחה, חשוב שתכירו את הנושא כמו שצריך – בסיס טוב יכול רק לעזור.
מה זה בכלל לוג?
חוקי לוגריתמים, הם חוקים שנבצע על לוגים.
כלומר, בשביל להבין את החוקים, כדאי שנבין בכלל מה הוא לוג.
לוג (log), היא פונקציה מתמטית בסיסית, כמו חיבור, חיסור, כפל או חילוק.
במילים פשוטות – היא הפעולה ההפוכה לחזקה.
כשנתונים לכם שני מספרים – הפעולה לוג תחשב את מעריך החזקה בו עשיתם שימוש בשביל להגיע ממספר אחד לאחר.
למשל – במידה ויש לי את המספר שתיים והמספר שמונה – אקבל במחשבון שלי בפעולת לוג את המספר שלוש.
למה? כי שמונה שווה לשתיים בשלישית.
במילים אחרות, זוהי הגדרת הפעולה לוג:
![]()
בשביל לבצע שימוש בפעולה לוג, תצטרכו להקיש על המקש הרלוונטי ולהזין שני מספרים:
- בסיס הלוג (המספר הקטן)– המספר שיועלה בחזקה.
- המספר שבתוך הלוג (המספר הגדול) – המספר שהועלה בחזקה.
התשובה שתתקבל כאמור, תהיה החזקה עצמה.
כך חישוב של לוג במחשבון לדוגמא אמור להיראות:
![]()
ומה עם לאן (ln) ולוג בלי בסיס?
מדובר באותה הגברת בשינוי האדרת. לאן ולוג בלי בסיס הם מקרים ספציפים של הפונקציה לוג:
Log בלי בסיס – יהיה לוג על בסיס 10.
Ln – מדובר בלוג על בסיס e.
במידה ועוד לא למדתם על הקבוע e, תתעלמו מההתייחסות לפונקציה לאן במאמר זה, כנראה הקדמנו עבורכם את המאוחר.
במילים אחרות, כשאתם מבצעים שימוש במחשבון בפונקציית לוג או לאן, תידרשו לשים רק מספר אחד – המספר הגדול, שהועלה בחזקה.
זאת כיוון שהמספר הקטן כבר נתון לנו לפי ההגדרה של לאן ולוג.
תחום הגדרה של לוג
לפני שאנחנו ניגשים לחוקי לוגריתמים חשוב לקחת בחשבון את תחום ההגדרה של הפונקציה:
בסיס הלוג (a) – בסיס הלוגריתם חייב להיות חיובי ושונה מאחד.
המספר שבתוך הלוגריתם (b) – כיוון שבסיס הלוגריתם חיובי בהתאם לכך גם המספר שבתוך הלוג צריך להיות חיובי.
חשוב! –כשאתם באים לפתור משווה לוגריתמית, חשוב שבהתאם לתחום ההגדרה של פונקציית הלוג תגדירו את הערכים בהם המשתנה x אינו מוגדר – כך תוכלו לשלול פתרונות במידת הצורך ולוודא שאתם מגיעים לתשובה הנכונה.
ועכשיו, לכללי לוגים
עכשיו כשאתם מכירים את העולם הזה קצת יותר מקרוב, ישנם כמה כללים שחשוב שתכירו.
הכללים נועדו להקל עליכם לא בחישובים במחשבון, אלא במשוואות לוגריתמיות, בהן תידרשו למצוא משתנים.
עם טריקים פשוטים תוכלו לבסוף לבוסס את איקס ולמצוא את ערך המשתנה.
בבוא הזמן תידרשו גם לדעת לחקור פונקציות לוגריתמיות ובקיצור אם אתם שואלים אותנו – למידה של כללי לוגים היא בסיסית והכרחית להצלחה בתוכנית הלימודים כפי שהיא נראית כיום.
אז אלו חוקי לוגים חשוב שתכירו?
![]()
![]()
![]()
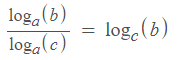
![]()
![]()
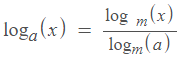
תרגילים לדוגמא
תרגיל א'
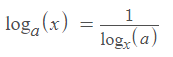
פתרון:
מדובר בתרגיל בסיסי במיוחד עם חוקי לוגריתמים.
נחזור להגדרת פונקציית לוג:
![]()
כעת, נתבונן במשוואה שקיבלנו:
a – בסיס הלוג שלנו הוא 3.
b – הערך של b הוא 4x + 1
c – שווה ל-2.
כעת נוכל לפתור את המשוואה:
![]()
![]()
וסיימנו!
תרגיל ב'
![]()
פתרון
נוציא מכנה משותף לאיברים:
![]()
כעת יש לנו שני פתרונות –
![]()
![]()
![]()
ומכאן –
![]()
תרגיל ג'
![]()
על מנת לפתור את התרגיל נזכר באחד מכללי הלוגים הראשונים שלמדנו:
![]()
כלומר, את שתי פונקציות הלאן שלנו, נוכל באמצעות הכלל הפשוט הזה לאחד לאחת באופן הבא:
![]()
ועכשיו, באמצעות הגדרת הלוג נוכל למצוא את x:
![]()
![]()
נמצא את ערכי האיקס:
![]()
ומה עכשיו?
חוקי לוגריתמים הוא נושא לא יותר מידי אינטואטיבי בהתחלה – המונחים חדשים, הסימונים לא מוכרים ובגדול, מדובר בתחום שעוד לא יצא לכם להכיר מקרוב.
במידה והיה מדובר בתחום קטן ושולי, הייתם אולי יכולים לדחוק אותו לפינה, אבל במקרה הזה – מדובר בנושא משמעותי במיוחד.
בידע הבסיסי שלכם בחוקי לוגריתמים תיעזרו על מנת לפתור משוואות מורכבות ולחקור פונקציות לוגריתמיות.
ולכן, אם אתם שואלים אותנו – חשוב שתשבו על החומר כמו שצריך ותבינו אותו לעומק.
אנחנו ממליצים לכם לעבור על ההסברים שלנו שוב בראש נקי, לתרגל את כל התרגילים שיש לכם בנושא בספר ולשבת עם חברים ולחלוק איתם שיטות וגישות שונות לפתירת התרגילים – אין דרך אחת לפתור כל תרגיל, ככל שתראו יותר דרכים כך יהיה לכם קל יותר לגשת לתרגילים הבאים.
ומה אם בכל זאת קשה לי?
כיום, שיעורים פרטיים במתמטיקה הפכו לנפוצים במיוחד והאמת היא שזה לא ממש מפתיע – תוכנית הלימודים עמוסה לעייפה ותלמידים רבים מוצאים את עצמם מתקשים וצוברים פערים במהלך שנת הלימודים.
אם אתם מתקשים עם החומר הנלמד, מחפשים תמיכה נוספת או פשוט רוצים להגיע למבחן מוכנים באופן הטוב ביותר – הגעתם למקום הנכון.
אצלנו באתר תוכלו למצוא מגוון רחב של מורים פרטיים במתמטיקה שיכולים לעזור לתלמידים בכל הכיתות והרמות.
רמת השיעורים תותאם לרמה שלכם, לצרכים שלכם ולקצב ההתקדמות האישי שלכם.
כך תוכלו להיות בטוחים שאתם מקבלים את המעטפת הכי טובה שאפשר ולהגיע למבחן בלב שקט.


