נוסחת השורשים לפתרון משוואה ריבועית

עכשיו כשאתם יודעים מה מחכה לכם, אפשר להתחיל לגשש באפלה.

כשאנחנו פונים לפתירת משווה ריבועית, נעביר ראשית את כל האיברים לאותו האגף.

באופן כללי, נקבל כנראה את התצורה הבאה:

לפני שנפנה לנוסחת השורשים, נבצע כמה הגדרות בסיס:

a – יהיה המקדם של איקס בריבוע. למשל, ב-, ה-a שלנו יהיה שווה ל-3.

b – יהיה המקדם של איקס בתצורתו הרגילה. למשל, ב-6x, ה-b שלנו יהיה שווה ל-6.

c – יהיה האיבר החופשי, מספר רגיל שלא תלוי באיקס. למשל, 6 או 8.

דלתא – האזור שתחום בשורש בתוך נוסחת השורש נקרא בדיבור המתמטי דלתא. 

אנחנו מזהירים אתכם, נוסחת השורשים לא תיראה לכם כל כך יפה בהתחלה, אבל אולי עדיף פשוט להוריד את הפלסטר:

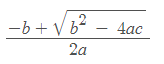
הנוסחה אמנם נראית בהתחלה באמת ממש לא סימפטית, אבל עם קצת תרגול – היא נגישה ונוחה למדיי. 

כמה דברים שחשוב לזכור!

• שני פתרונות – בפתרון המשוואה שלכם לעומת משוואות רגילות ממעלה ראשונה אתם תקבלו שני פתרונות – לכן ישנו הסימון של הפלוס מינוס לפני השורש.
• דלתא גדול או שווה לאפס – כיוון שאזור הדלתא תחום בשורש, חשוב לזכור שערכים נמוכים מאפס שיהיו בתוכו לא יובילו לשום פתרון.

כלומר, במצב בו הגעתם לערך שלילי מתחת לשורש – אין לכם פתרון למשוואה.

למצב כזה יכולות להיות שתי סיבות:

• למשוואה אין פתרון – הפונקציה שאתם חוקרים לא מוגדרת בנקודה נתונה מסוימת, המשוואה שקיבלתם לא פתירה. 
• ביצעתם טעות חישוב – במידה וקיבלתם תרגיל במבחן שבוחן את הידע שלכם בפתירת משוואה ריבועית, סביר שיביאו לכם משוואה עם פתרון.

לפני שאתם מגיעים למסקנה שמדובר במשוואה בלי פתרון, תוודאו את עצמכם, תחזרו כמה שלבים אחורה ותבחנו את ההצבה שלכם בנוסחת השורש ובמחשבון.

• מספרים "מגעילים" – הרבה תלמידים לא אוהבים את נוסחת השורש בגלל שהיא יכולה להיות מלחיצה.

הרבה פעמים מספר "יפה" עגול או יחסית ברור נחשב כנכון בעיניי התלמידים ואילו המספר ה"מגעיל" ייחשב כטעות.

אמנם מורים רבים כנראה ישמחו ויעדיפו להביא לכם תרגילים עם פתרונות נחמדים אבל תשובה שהיא מספר לא שלם היא לא בהכרח לא נכונה.

במילים אחרות – מה שיקבע בסופו של דבר את התקפות של הפתרון שלכם יהיה הדרך שבה הגעתם אליהם ולא התשובה המספרית הסופית, לא לדאוג.

• קחו את הזמן – כיוון שמדובר בנוסחה מעט מורכבת במיוחד בהתחלה, חשוב שתקחו את הזמן בפתרון התרגילים בשביל לוודא שאתם לא נופלים על טעויות חישוב שלא נובעות בפער הבנתי. 

תרגיל לדוגמא

פתור את המשוואה הבאה:

פתרון

במבט זריז נראה כי מדובר במשוואה מפחידה במיוחד!

אבל האמת היא, שהמצב יותר פשוט ממה שהייתם מצפים.

בשביל להפוך את המשוואה המורכבת הזאת לפתירה, כל מה שנצטרך לעשות זה להוציא גורם משותף X:

כרגע למשוואה שלנו יש שני פתרונות אפשריים:

• X = 0
• 

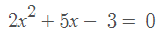
וכמו שאתם רואים – כעת נתונה לנו משוואה ריבועית!

בשביל לפתור אותה, כל מה שאנחנו צריכים לעשות עכשיו זה פשוט להציב את הערכים בנוסחת שורשים:

• a = 2
• b = 5
• c = -3

כעת, נציב בנוסחה:

נסדר קצת את האיברים: 

ונמצא את שני הפתרונות שלנו:

וזהו! סיימנו!

הפתרונות למשוואה שלנו הן:

• x = 0
• x = 0.5
• x = -3