איך מחשבים שטח משולש?
מבט מהיר על איך מחשבים שטח משולש?
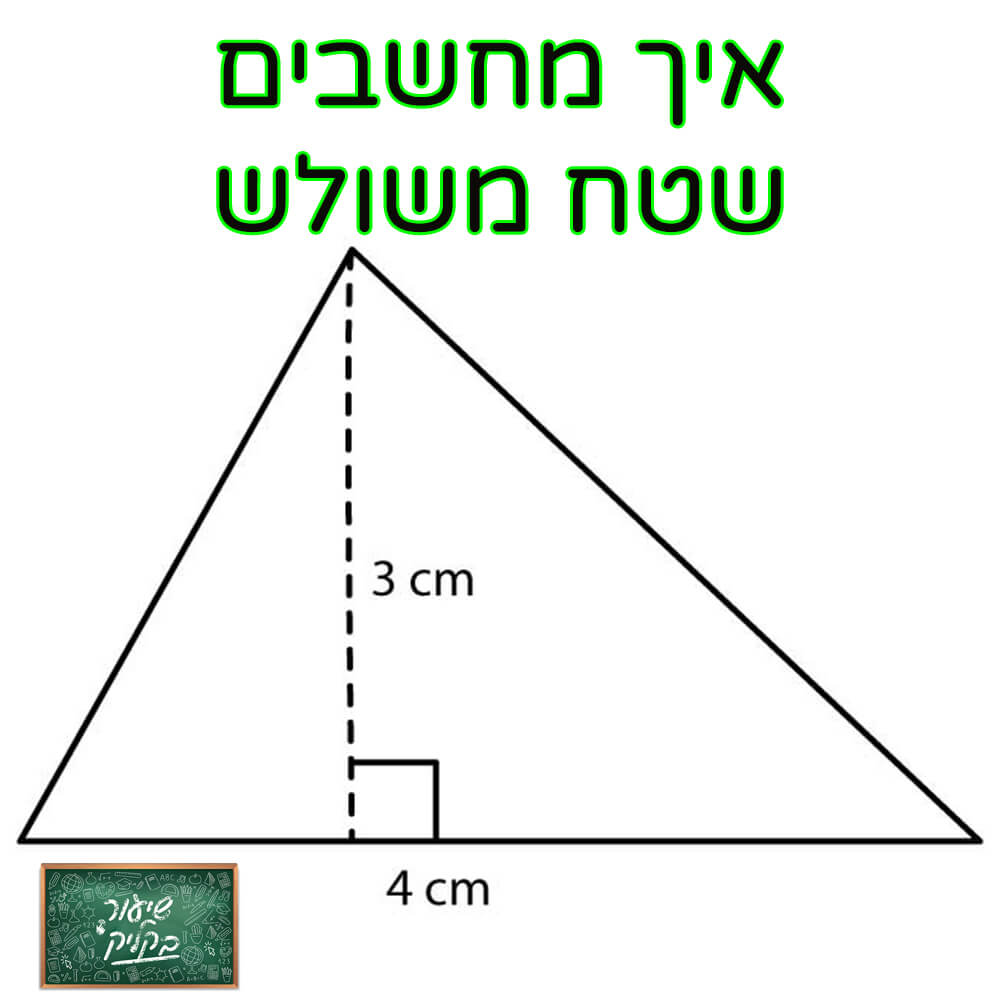
מתי נרצה לחשב שטח משולש?
אם אתם תלמידי תיכון ואפילו סטודנטים באוניברסיטה, חישוב של שטח משולש הוא ללא ספק מיומנות הכרחית.
לצד היכולת לבצע חילוק ארוך או לזכור את לוח הכפל, מיומנות חישוב השטח יכולה לשמש אתכם במגוון רחב של אופנים.
אם אתם חושבים יום אחד לבנות מכונית לגמרי בעצמכם או להנדס מוצר משלכם – כנראה שמדובר באחת ממיומנויות הבסיס שאתם צריכים להשיג לפני שאתם מתחילים את הדרך הארוכה שלכם.
בתיכון, חישובי שטחי משולש שימושיים בעיקר לתרגילים בגיאומטריה וטריגונומטריה.
התרגילים שתקבלו כנראה לא יתמקדו בחישוב השטח עצמו – בחלק מהמקרים יהיה מדובר בכלי שיעזור לכם להשיג פרטים נוספים ובמקרים אחרים, עיקר האתגר יהיה בהשגת הפרטים שיאפשרו לכם לבצע את החישוב.
במילים אחרות, ברגע שאתם מכירים את המיומנות הזאת, מאוד קל ליישם אותה והיא חד משמעית תשדרג בכמה וכמה רמות את היכולת שלכם לפתור תרגילים ובתכלס, לא מדובר בעניין יותר מידי מסובך.
אילו סוגי משולשים יש?
לפני שנתחיל בכלל לדבר על החישובים עצמם, ישנם כמה דברים שאתם צריכים להכיר. ראשית, יהיו כמובן סוגי המשולשים שיכולים לעמוד מולכם. באופן כללי, במשולש יש 180 מעלות ותכונות המשולש נגזרות מהאופן שבו אלה מחולקות בין הזווית השונות בו. בסך הכל ישנם שלושה סוגים שונים של משולשים שיכולים להתקיל אתכם, לא יצליחו לתפוס אתכם לא מוכנים:
- משולש ישר זווית – משולש בעל זווית ישרה אחת (בעלת 90 מעלות) ושתי זוויות חדות (בעלות פחות מ-90 מעלות)
- משולש קהה זווית – משולש בעל זווית קהה אחת (בעלת יותר מ-90 מעלות) ושתי זוויות חדות.
- משולש חד זווית – משולש בעל שלוש זוויות חדות.
האמת היא, שישנן דרכים נוספות לחלק את אוכלוסיית המשולשים המיוחדת. לא נרחיב על כך במאמר זה, אבל שימו לכם בראש שמונחים כמו משולש שווה צלעות, משולש שווה שוקיים ומשולש זהב כנראה עוד יפגשו אתכם לאורך הדרך.
אילו מונחים כדי להכיר?
עכשיו כשאתם מכירים את סוגי המשולשים השנים, אפשר לצלול למונחים קצת יותר ספציפיים, שיעזרו לכם בביצוע החישוב עצמו.
הנה הם כמה מונחים, שכנראה יעזרו לכם בביצוע החישובים:
- צלע נגדית – צלע שנמצאת מול קודקוד ולא נפגשת איתו.
- גובה – גובה יהיה קו שנוריד מאחד מקודקודי המשולש וייצור זווית ישרה עם הצלע הנגדית אליה יורד.
בחלק מהמקרים הגובה לא "ייגע" ישירות בצלע, אלא בהמשך שלה – נרחיב על כך בהמשך, לא לדאוג.
- תיכון – קטע שיוצא מקודקוד משולש אחד וחוצה את הצלע הנגדית לשני חלקים שווים.
- חוצה זווית – מדובר בקו שיוצא מקודקוד המשולש וחוצה בו את הזווית לשתי זוויות שוות בגודלן.
- משפט פיתגורס – במשולש ישר זווית, במידה ויש לנו שתיים מתוך שלוש צלעות המשולש נוכל בקלות לחשב את הצלע השלישית.
- ניצב – צלע שיוצרת עם צלע נוספת זווית ישרה. נגדיר, הניצבים במשולש שלנו הם a, b.
- יתר – הצלע הנמצאת מול הזווית הישרה. נגדיר, היתר במשולש שלנו הוא c.
משפט פיתגורס אומר את הדבר הבא:
![]()
סינוס הזווית – פונקציה טריגונומטרית פשוטה שמשמשת אותנו לחישובי זוויות. במידה ואתם לא לומדים טריגונומטריה – המונח והנוסחה הטריגונומטרית לא רלוונטית עבורכם!
אז באילו דרכים אפשר לחשב שטח משולש?
עכשיו כשאתם מכירים את המונחים כמו שצריך, אנחנו חושבים שאפשר להתחיל בבלגן!
בתכלס, יש רק שתי נוסחאות לחישוב שטח משולש, כאשר אחת מהן רלוונטית כנראה עבור כולכם והשנייה יכולה לשמש את אלו מכם שהתחילו כבר ללמוד טריגונומטריה.
בסופו של דבר, שתי הנוסחאות יביאו אתכם לאותה התוצאה בדיוק – בחירת הנוסחה תוכל להיעשות על בסיס טעמי נוחות אבל במרבית המקרים תהיה פשוט תלויה בנתונים שסיפקו לכם.
חישוב גיאומטרי בסיסי:
על מנת לחשב שטח של משולש, כל הפרטים שאתם צריכים הם רק גדלי צלע והגובה המסוים שיורד אליה.
כשמדובר במשולש ישר זווית, יהיה כמובן מדובר בשתי הצלעות שיוצרות את הזווית הישרה.
במקרים בהם מדובר במשולש חד זווית או קהה זווית – יינתן לכם גובה בשרטוט או שתצטרכו בעצמכם להוריד אותו.
נגדיר:
- צלע – תיקרא A
- הגובה לצלע – ייקרא B
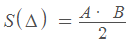
שאלה לדוגמא:
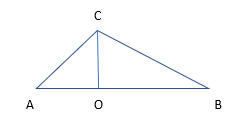
נתון לכם משולש קהה זווית (ABC), וגובה CO שיורד על הצלע.
נתונים נוספים:
- צלע AB = 9 ס"מ
- מקטע OA = 4 ס"מ
- צלע BC = 8 ס"מ
מצא את שטח משולש ABC (רמז – היעזר בנוסחת השטח הבסיסית).
פתרון:
בסופו של דבר, נשאף הרי לחשב את שטח המשולש באמצעות הנוסחה שקיבלנו.
כאשר נתון לנו צלע וגובה, ניתן להבין בקלות שהכיוון של השאלה הוא למצוא את הנתונים שיאפשרו לנו להשתמש בהם לחישוב השטח.
כלומר, אין צורך בבניות עזר נוספות, או מחשבה יותר מידי מסובכת
אז מה אפשר לעשות?
ראשית, נתון לנו כי מקטע OA שווה לארבע. הדבר הראשון שנעשה, יהיה למצוא את מקטע OB באמצעות החישוב הבא:
![]()
מכאן ניתן להסיק, כי קטע OB = 5 ס"מ.
ניגש למשפט פיתגורס – עכשיו כשיש לנו את מקטע OB, נוכל ביחד עם הנתון שקיבלנו על BC לחשב את הגובה לצלע AB.
זאת כמובן, בשביל להציב אותו בנוסחה לחישוב השטח.
ניגש לחישובים:
נציב:
![]()
![]()
נעביר אגפים:
![]()
לאחר חישוב זריז, נקבל לבסוף ש-CO בריבוע שווה 36 וכיוצא בזאת, הגובה CO שווה 6.
ניגש להצבה בנוסחה – עכשיו כשיש לנו את כל הפרטים, כל מה שנשאר לנו לעשות זה רק להציב את הנתונים בנוסחה האהובה שלנו.
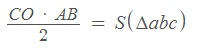
נציב ונקבל:
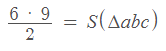
ובסיום החישובים, נבין כי שטח משולש abc שווה ל-27 סמ"ר.
זהו! סיימנו! זה לא היה כל כך מסובך, נכון?
הנוסחה הטריגונומטרית:
נוסחה שימושית לא פחות שיכולה חד משמעית להקל עליכם בתרגילי הטריגו המורכבים והלא נעימים היא ללא ספק הנוסחה הטריגונומטרית לחישוב שטח.
על מנת לחשב שטח משולש באמצעות הנוסחה, אנחנו זקוקים לנתוני שתי צלעות והזווית שכלואה בינהן.
נגדיר:
- צלע א' – a
- צלע ב' – b
- הזווית הרלוונטית – x
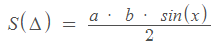
שאלה לדוגמא:
נתון משולש ABC.
- cba = 58>
- cab = 62>
- 5 ס"מ = צלע BC
- 2 ס"מ = קטע A0
- 3 ס"מ = גובה CO
מצא את שטח משולש ABC באמצעות הנוסחה הטריגונומטרית לחישוב שטח.
פיתרון:
ראשית, נבחין בפרטים שקיבלנו.
נתון לנו גובה נחמד, נתונה לנו צלע ונתון לנו מקטע מהבסיס.
כבר נבהיר – יש לוודאי כמה דרכים לגשת לתרגיל הזה ולפתור אותו, נלך בדרך הראשונה שעלתה לנו לראש.
נתחיל בלחשב את הצלע AC – נתון לנו הגובה CO, נתון לנו המקטע AO ומדובר במשולש ישר זווית.
מה זה אומר? פיתגורס כמובן:
![]()
נציב ונקבל:
![]()
ומכאן:
![]()
כעת כשיש לנו את צלע BC ואת הצלע AC, כל מה שחסר לנו בשביל לבצע שימוש בנוסחה זה רק הזווית acb> שעומדת בינהן
באמצעות הנתונים על שתי הזוויות האחרות נוכל לחשב את הזווית:
![]()
מחישוב זריז נקבל כי זווית
כעת, כל מה שנותר לנו לעשות זה רק לבצע שימוש בנוסחה:

נציב:
![]()
ונקבל:
![]()
ומה עכשיו?
עכשיו כשאתם מכירים קצת יותר את הנוסחאות, לא סיימתם את העבודה.
בשביל לקבל ציונים טובים במבחן חשוב לא לדחות את הלימודים לרגע האחרון. תעברו על הדוגמאות ועל ההסברים שלנו, תפתרו כמה תרגילים בעצמכם והכי חשוב – תוודאו שהבנתם הכל.
אנחנו מאמינים שלמידה מעמיקה וטובה צריכה להיעשות בהדרגה ובעקביות.
אל תדחו את הכל לרגע האחרון – תתחילו ללמוד עוד היום.
על המורים הפרטיים שלנו אגב, שמעתם?
אם אתם מרגישים שאתם זקוקים לתמיכה נוספת, הם יותר מישמחו לעזור.


